数字签名最常用的实现方法_数字签名最常用的实现方法建立在什么

数字签名最常用的实现方法_数字签名最常用的实现方法建立在什么

       数字签名最常用的实现方法的今日更新是一个不断发展的过程，它反映了人们对生活品质的不断追求。今天，我将和大家探讨关于数字签名最常用的实现方法的今日更新，让我们一起感受它带来的高品质生活。

1.ECDSA（椭圆曲线数字签名算法）

2.电子签名的实现方式主要有哪几种

3.数字签名怎么做？

4.在数字签名中发送方使用什么进行数字签名

ECDSA（椭圆曲线数字签名算法）

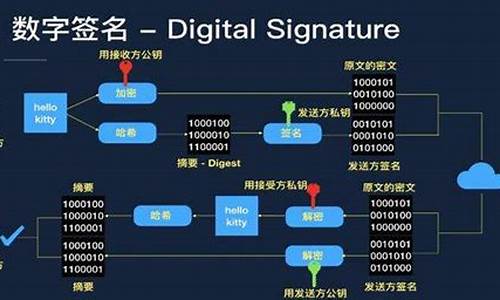
        ECDSA（Elliptic Curve Digital Signature Algorithm）

        在现实工作和生活中，我们使用签名的方式表达对一份文件的认可，其他人可以识别出你的签名并且无法伪造你的签名。数字签名就是对显示签名的一种电子实现，它不仅可以完全达到现实签名的特点，甚至能够做的更好。

        常用的数字签名算法有RSA（Rivest-Shamir-Adleman Scheme）、DSS（Digital Signature Standard）等。比特币使用ECDSA来生成账户的公私钥以及对交易和区块进行验证。

        1.Alice（密码学中常用A到Z开头的人名代替甲乙丙丁等，字母越靠后出现频率越低）生成一对密钥，一个是sk（signing key），是非公开的；另一个是vk（verification key），是公开的。

        这一对密钥同时生成，并且在数学上是相互关联的，同时，根据vk无法推测出关于sk的任何信息。

        2.数字签名算法接收两个输出：信息M和sk，生成一个数字签名Sm

        3.验证函数接收信息M、Sm以及vk作为输入，，返回结果是yes或者no。这一步的目的是为了验证你看到的针对信息M的数字签名确实是由Alice的sk来签发的，用于确认信息与签名是否相符。

        与手写签名不同，手写签名基本都是相似的，但是数字签名却受输入影响很大。对输入轻微的改变都会产生一个完全不同的数字签名。一般不会对信息直接进行数字签名，而是对信息的哈希值进行签名。由加密哈希函数的无碰撞性可知，这样和对原信息进行签名一样安全。

        在数学上，任何满足以下方程的点所形成的曲线称为随机椭圆曲线： 并且 ，a和b可以为任意值。下面展示几个随机椭圆函数的示例：

        在了解如何通过基于secp256k1椭圆曲线的ECDSA算法生成公私钥之前，我们需要了解在随机椭圆曲线里，点的加法是如何实现的。

        首先定义椭圆曲线上点的加法。设椭圆曲线上有两点，A和B点，那么作过这两点的直线与该曲线相交于第三点（C点），然后关于X轴对称得到D点，则D为这两个点的和，记作D=A+BD=A+BD=A+B。很明显，D点也在该曲线上。所以椭圆曲线上两点之和也是曲线上的点。

        特例：

        1.如果两点重合，则做该点的切线，与曲线相交点的对称点为和，即A+A=C

        如图：

        有了加法以后，乘法实现是不过是进行多次加法运算。有了一个基准点P以后，我们可以对其进行乘法运算，最后可以得到曲线上的另外一个点。

        设PPP是椭圆曲线上的一个点，那么正整数kkk乘以点PPP的结果由下面的式子定义，注意式子中的加法是上面提到的椭圆曲线上点的加法：

        点的运算满足结合律：

        很显然，通过累加 的方式计算 是一种很笨的办法，其时间复杂度是线性的。上面我们提到过，椭圆曲线上点的加法是满足结合律的，即 ，扩展一下，就有

       

        于是就有这么一种骚操作，比如计算 ，我们可以先计算 ；然后计算 ；再计算 ；最后计算 。这里我们把15次加法减少到了4次。

        当然，k的值不可能总是2的幂。实际上上面的操作可以推广到k为任意正整数的情况。比如计算23P，首先计算 ，然后

        因为 ，所以 。总共只需要7次加法。

        分析一下，对于任意正整数k，我们都可以利用这个方法将计算k?P所需的加法计算次数降低到

        也就是说，从时间复杂度的角度来看，这个算法是一个 的算法。

        这个方法被称为快速幂算法，原本常用于快速计算某个数的k次幂，这里将其推广到椭圆曲线点乘的快速计算中。

        为什么要在介绍了椭圆曲线上点的乘法后突然冒出一个快速幂算法？快速幂算法对于椭圆曲线加密有什么意义？因为数学家/密码学家发现，利用快速幂算法计算 的时间复杂度是对数级的，但是要在知道 和 的前提下，倒推出 的值，没有比挨个尝试 的值快太多的算法。于是椭圆曲线加密依赖的数学难题就这么诞生了。

        如果我们改一种记法，把椭圆曲线上点的加法记作乘法，原来的乘法就变成了幂运算，那么上述难题的形式跟离散对数问题应该是一致的。即：

        所以这个难题叫椭圆曲线上的离散对数问题。

        尽管两者形式一致，但是他们并不等价。实际上这个问题比大整数质因子分解（RSA）和离散对数（DH）难题都要难得多，目前还没有出现亚指数级时间复杂度的算法（大整数质因子分解和离散对数问题都有），以致于同样的安全强度下，椭圆曲线加密的密钥比RSA和DH的短不少，这是椭圆曲线加密的一大优势。

        设随机取一个 ~ 位之间的值x，计算 ，最后的结果一定会落在曲线上的一点。设该点为 ，在公开 以及具体曲线的方程的情况下，能否反推出最初的随机值 ？

        证：寻找 的过程只能通过暴力计算， 的可能值为 ~ 中的一个，平均来说需要计算 次能够找到一次 值。那么问题来了，运行一次 的计算需要多长的时间呢？

        设我们使用的是超级计算机，主频为 （一秒钟可以进行一万亿次运算），从宇宙诞生的那一刻开始计算，到现在也就进行了 次。找到 值的概率为 。这个概率和下一秒地球被巨型陨石撞击而毁灭的概率接近，既然我们读到了这里，那么说明这件事没有发生。

        在上面的案例中， 是 ~ 位的一个随机数，可以作为私钥。 是随机椭圆曲线上的一个点，也就是由私钥生成的公钥，因此优点可以1得证。

        但是密码学中，并不能使用上面介绍的实数域上的椭圆曲线。因为

        所以我们需要引入有限域上的椭圆曲线。

        要证明优点2，还需要将随机椭圆曲线做一些改动：为了保证最后计算出来的点的坐标值相加是512位，secp256k1引入了一个对质数取模的机制。具体来说，随机椭圆曲线从

        变为了 其中 ，是小于 的最大质数。

        此时的随机椭圆曲线函数图如下：

        具体来说，就是向别人证明我知道 ，但不暴露 的任何信息。（有些类似于零知识证明）

        证：前面介绍过结合律： 添加一个hash函数，简单修改可以得出： 使 ，那么可知 为 。此时方程为： 为了简单起见，我们记 和 。此时方程化简为： 上面这个方程是什么意思呢？

        可以这样设：在已知 的情况下，如果能够提供一个 和 满足上面的方程，就可以证明一个人拥有 。这个设有一个前提，如果一个人不知道x，那么他就无法提供 和 满足上面的等式。

        详细探讨这个前提：如果一个人不知道x，又想计算出 和 ，能够办到吗？结论是不能，首先我们无法从 计算出 （在有限时间内）。

        还有一个问题：在已知 和 的情况下，能否计算出关于 的任何信息？

        根据公式： 只要解出 就可以了。

        要想计算出x，就需要知道r，但是在r没有公开的情况下，有什么办法可以计算r吗？我们知道R=r*P；但是根据这个公式无法倒推出r（刚才介绍的那个数学难题），所以x也是安全的。

        至此，可以证明算法的第二个优点。

电子签名的实现方式主要有哪几种

       公开密钥密码不仅能够实现数字签名，而且安全方便而且相比于传统密码更容易达到书面签名的效果，所以公开密钥密码深受欢迎！

       由于数字签名的形式是多种多样的，比如有通用数字签名，仲裁数字签名，不可否认签名，盲签名，群签名，门限签名等，在这里我就以数字签名的一般方法解答吧！

       (1)A和B都将自己的公开密钥Ke公开登记并存入管理中心的共享的公开密钥数据库PKDB,以此作为对方及仲裁者验证签名的数据之一。

       （2）A用自己的保密的解密密钥Kda对明文数据M进行签名得到签名S，然后A查询PKDB查到B的公开的加密钥Kea，并对用Kea对S再加密，得到密文C

       （3）最后A把C发送给B，并将S和C留底。

数字签名怎么做？

       电子签名的实现方式有：文档电子签名软件和使用数字证书对Word文档进行数字签名。

       文档电子签名软件是一种电子盖章和文档安全系统，可以实现电子盖章(即数字签名)、文档加密、签名者身份验证等多项功能。对于签名者的身份确认、文档内容的完整性和签名不可抵赖性等问题的解决具有重要作用。使用数字证书对Word文档进行数字签名，保证签名者的签名信息和被签名的文档不被非法篡改。签名者可以在签名时对文档签署意见，数字签名同样可以保证此意见不被篡改。

在数字签名中发送方使用什么进行数字签名

       首先我们要明确一个观念，数字签名是实现电子签名的国际通用的手段，而在实践中，我们往往把数字签名与电子签章电子签名之间画上等号。因而，要问如何进行数学签名，其实也就是在问如何进行电子签章电子签名

       我以微签为例子吧，简单的几步就可以进行电子签章。

       1登录微签电子签章平台，用手机号免费注册登录：

       2：第一步，我们需要把印章或者签名导入系统中。预先把印章或者签名盖在白纸上，扫描进电脑保存为印章或者签名大小的方形。可以为bmp或png格式，注意印章或者签名底色务必为白色。

       另外注意印章或者签名的分辨率务必为192像素，这样能确保电子印章或者签名与实体章或者签名一样大小。

       第二步，我们需要把印章或者签名导入微签系统中。在“系统管理”>“签章管理”里的新增签章。

       把前面扫描的印章或者签名导入进来，给印章命名，设置密码，授权给谁谁可以使用。如果你申请了数字证书，也可以绑定证书，用Ukey来验证盖章。

       第三步，进入主题，要盖章了。微签的电子签章，可以在审批流程中盖章，也可以直接上传文件盖章，看你如何设置权限。

       本次以直接添加文件盖章为例，从“文件签章”>“我要签章”，上传需要盖章的文件：

       点“现在签章”，打开签章编辑器界面。先盖单个印章：

       若是多页文件，需要再盖个骑缝章：

       个人签名怎么办？不急！

       在PC端，你可以如以上电子印章的步骤一样，导入签名。

       在移动端，你可以直接在手机屏幕上手写。

       最后一步，合同盖好章了，何去何从？

       电脑上，你可以在线直接发邮件、转发、下载、归档：

       手机上，就更方便了，你可以把合同直接发微信、发QQ给客户：

       是不是非常方便快捷呢？电脑端和手机端都可以使用，说再多也不如您亲自上微签免费注册一个账号来的实在，“纸上得来终觉浅，得知此事要躬行。“亲自体验一下数字签名怎么做。

在数字签名中，发送方使用发送方的私钥进行数字签名。 数字签名(也称公钥数字签名)是只能由信息的发送者生成的数字串，他人无法伪造。这个数字串也是信息发送者发送信息真实性的有效证明。它是一种认证数字信息的方法，类似于写在纸上的普通物理签名，但利用公钥加密领域的技术实现。一组数字签名通常定义两个互补的操作，一个用于签名，另一个用于验证。数字签名是非对称密钥加密技术和数字摘要技术的应用。简单来说，所谓的数字签名就是附加在数据单元上的一些数据或者对数据单元进行的密码变换。这种数据或转换允许数据单元的接收方确认数据单元的来源和完整性，并保护数据不被人(如接收方)伪造。这是一种签署电子消息的方法，并且签署的消息可以在通信网络中传输。数字签名既可以基于公钥密码体制获得，也可以基于私钥密码体制获得，主要是基于公钥密码体制的数字签名。包括一般数字签名和特殊数字签名。常见的数字签名算法有RSA、ElGamal、Fiat-Shamir、Guillou-Quisqour、Schnorr、Ong-Schnorr-Shamir、Des/DSA、椭圆曲线数字签名算法和有限自动机数字签名算法。特殊数字签名包括盲签名、代理签名、群签名、不可否认签名、公平盲签名、门限签名、具有消息恢复功能的签名等。它与具体的应用环境密切相关。显然，数字签名的应用涉及法律问题，美国联邦基于有限域上的离散对数问题制定了自己的数字签名标准(DSS)。

       今天关于“数字签名最常用的实现方法”的讨论就到这里了。希望通过今天的讲解，您能对这个主题有更深入的理解。如果您有任何问题或需要进一步的信息，请随时告诉我。我将竭诚为您服务。